Построение графика квадратичной функции (продолжение)

Построение графика квадратичной функции. § 3. Квадратичная функция и ее график. Алгебра 9 класс. Макарычев. Онлайн учебник

§ 3. Квадратичная функция и ее график

Построение графика квадратичной функции (продолжение)

Пример 3. Построим график 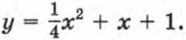функции

Графиком функции 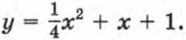является парабола, ветви которой направлены вверх. Найдем координаты ее вершины:

Вычислив координаты еще нескольких точек, получим таблицу:

График функции 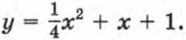изображен на рисунке 33.

Упражнения

120. Тело брошено вертикально вверх с начальной скоростью υ₀ (м/с) с высоты h₀ (м). Высота h (м), на которой окажется тело через t (с), выражается формулой

На рисунке 34 показан график зависимости h от t для случая, когда h₀ = 20, υ₀ = 15.

Найдите по графику:

• а) сколько времени тело поднималось вверх;
  
  б) сколько времени оно опускалось вниз;
  
  в) какой наибольшей высоты достигло тело;
  
  г) через сколько секунд тело упало на землю.

121. Квадратичная функция задана формулой:

• а) у = х² – 4х + 7;
  
  б) у = -2x² – 5x – 2.

Найдите координаты вершины параболы. Наметив на координатной плоскости вершину параболы и ее ось симметрии, изобразите схематически график.

122. Постройте график функции у = -х² + 2х + 8 и найдите, используя график:

• а) значение функции при х = 2,5; -0,5; -3;
  
  б) значения аргумента, при которых у = 6; 0; -2;
  
  в) нули функции и промежутки знакопостоянства;
  
  г) промежутки возрастания и убывания функции, область значений функции.

123. Постройте график функции у = 2x² + 8х + 2 и найдите, используя график:

• а) значение у при х = -2,3; -0,5; 1,2;
  
  б) значения х, при которых у = -4; —1; 1,7;
  
  в) нули функции и промежутки знакопостоянства;
  
  г) промежутки возрастания и убывания функции, наименьшее значение функции.

<<< К началу          Окончание >>>