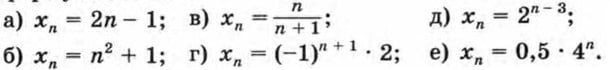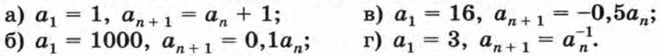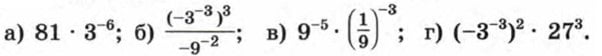Последовательности (окончание)

Последовательности. § 9. Арифметическая прогрессия. Алгебра 9 класс. Макарычев. Онлайн учебник

§ 9. Арифметическая прогрессия

Последовательности (окончание)

Упражнения

560. Выпишите первые несколько членов последовательности натуральных чисел, кратных 3, взятых в порядке возрастания. Укажите ее первый, пятый, десятый, сотый и n-й члены.

561. Известно, что (с_n) — последовательность, все члены которой с нечетными номерами равны -1, а с четными равны 0. Выпишите первые восемь членов этой последовательности. Найдите с₁₀, с₂₅, с₂₀₀, с₂₅₃, с_2k, c_{2k + 1} (k — произвольное натуральное число).

562. Пусть (а_n) — последовательность квадратов натуральных чисел. Выпишите первые десять ее членов. Найдите а₂₀, а₄₀, аn.

563. Какой член последовательности а₁, а₂, а₃, … :

• а) следует за членом а₉₉, а₂₀₀, а_n, а_{n + 1}, а_{n + 1}, а_2n;
  
  б) предшествует члену а₇₁, а₁₀₀, а_{n – 2}, а_{n + 3}. а3_n?

564. Перечислите члены последовательности (х_n), которые расположены между:

• а) x₃₁ и х₃₅; б) х_n и х_n+6; в)х_{n – 4} и х_n; г) х_{n – 2} и х_{n + 2}.

565. Найдите первые шесть членов последовательности, заданной формулой n-го члена:

567. Последовательность (а_n) задана формулой а_n = n² – n – 20. Укажите номера отрицательных членов последовательности и вычислите эти члены.

568. Вычислите второй, третий, четвертый и пятый члены последовательности (b_n), если известно, что:

• а) первый член равен 10, а каждый следующий на 3 больше предыдущего, т. е. b₁ = 10 и b_{n + 1} = b_n + 3;
  
  б) первый член равен 40, а каждый следующий равен предыдущему, деленному на 2, т. е. b₁ = 40 и

569. Выпишите первые пять членов последовательности (а_n), если:

570. Выпишите первые четыре члена последовательности (b_n), если:

• а) b₁ = 5, b_n+1 = b_n + 5; б) b₁ = 5, b_{n + 1} = b_n • 5.

Упражнения для повторения

571. Найдите пару положительных чисел х и у, удовлетворяющих уравнению х² + у² = 45, если известно, что у вдвое больше х.

572. Решите уравнение:

• а) 4х⁴ + 4х² – 15 = 0; б) 2х⁴ – х² – 36 = 0.

573. Решите неравенство:

• а) х² + х – 42 ≤ 0; б) (х + 11)(х + 4)(х – 1) > 0.

Представьте выражение в виде степени с основанием 3 и найдите его значение:

Ответы

• 566. а) 65; б) 230; в) 5150.

  567. а₁ = -20, а₂ = -18, а₃ = -14, а₄ = -8.

  571. х = 3, у = 6.

  572. a) ±√1,5; б) ±√4,5.

  573. а) [-7; 6]; б) (-11; -4) ∪ (1; +∞).

<<< К началу