§ 3. Что такое математическая модель (окончание) Алгебра 7 класс Мордкович
§ 3. Что такое математическая модель. Глава 1. Математический язык. Математическая модель. Алгебра 7 класс. Мордкович. Учебник
Глава 1. Математический язык. Математическая модель
Подведём итоги. В процессе решения задачи были чётко выделены три этапа.
-
Первый этап. Составление математической модели.
Второй этап. Работа с математической моделью.
Третий этап. Ответ на вопрос задачи.
Вот так обычно применяется математика к реальной действительности. После рассмотренного примера повторим вопрос: нужны ли математические модели и надо ли уметь работать с ними? Нужны! Разумеется, чем сложнее модель, тем больше фактов, правил, свойств приходится применять для работы с ней. Эти факты, правила, свойства надо изучить, что мы и будем с вами делать на протяжении всех лет изучения алгебры в школе.
Математические модели бывают не только алгебраические (в виде равенства с переменными, как в таблице на с. 17, или в виде уравнения, как было в примере 1). Для знакомства ещё с одним видом математической модели возьмём задачу из учебника математики для 6-го класса (специально берём задачу, с которой вы, может быть, встречались).
Пример 2. Построить график температуры воздуха, если известно, что температуру измеряли в течение суток и по результатам измерения составили следующую таблицу:

Р е ш е н и е. Построим прямоугольную систему координат. По горизонтальной оси (оси абсцисс) будем откладывать значения времени, а по вертикальной оси (оси ординат) — значения температуры. Построим на координатной плоскости точки, координатами которых являются соответствующие числа из таблицы. Всего получается 12 точек (рис. 1). Соединив их плавной линией, получим один из возможных графиков температуры (рис. 2). 
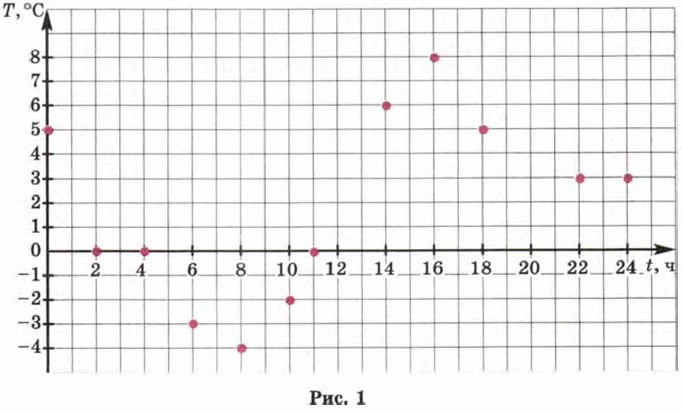
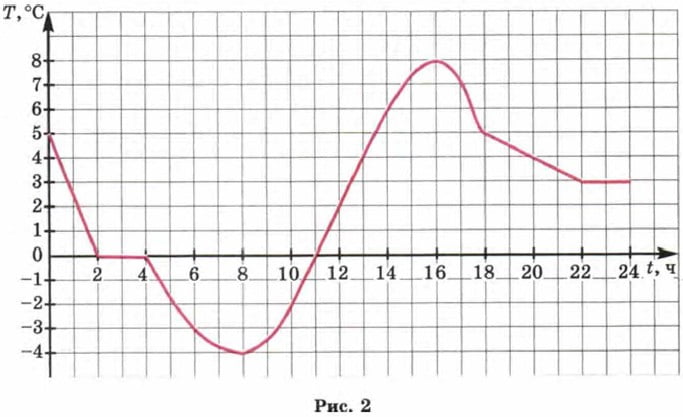
Построенный график есть математическая модель, описывающая зависимость температуры от времени. Анализируя этот график, можно описать словами, что происходило с температурой воздуха в течение суток. Ночью с 0 ч до 8 ч утра становилось всё холоднее (от 5° в 0 ч до -4° в 8 ч утра). Потом, видимо, выглянуло солнышко и стало теплеть, так что в 11 ч температура была уже не отрицательной, а нулевой (0°). До 16 ч теплело, причём в 16 ч было теплее всего (8°). А затем стало темнеть, температура начала постепенно снижаться и понизилась до 3° в 22 ч. Глядя на график температуры, можно приближённо определить, какая была наименьшая температура (-4° в 8 ч утра), какая была наибольшая температура (8° в 16 ч), где температура менялась быстрее, где медленнее, а где вообще не менялась (от 2 до 4 ч ночью и от 22 до 24 ч вечером). Рассмотренная математическая модель является примером графической модели.

Итак, нам нужно учиться описывать реальные ситуации словами (словесная модель), алгебраически (алгебраическая модель), графически (графическая модель). Бывают ещё геометрические модели реальных ситуаций — они изучаются в курсе геометрии. Впрочем, графические модели также иногда называют геометрическими, а вместо термина «алгебраическая модель» употребляют термин «аналитическая модель». Всё это — виды математических моделей.
Чтобы свободно оперировать любыми видами математических моделей, нужно научиться переходить от одного из них к другому. Так, выше, в примере 1, нам удалось перейти от словесных моделей к аналитическим (см. таблицу на с. 17). В примере 2 удалось перейти от словесной (точнее, табличной) модели к графической, что позволило вновь вернуться к словесному описанию рассматриваемой ситуации, но уже на более содержательном уровне. Будем учиться этим переходам.
-
Вопросы для самопроверки
1. Что такое математическая модель?
2. Какие виды математических моделей вы знаете? Приведите пример каждого вида математической модели.
3. Назовите три этапа математического моделирования.
4. На каком из этапов математического моделирования при решении текстовой задачи нам не нужно знать объекты условия задачи?