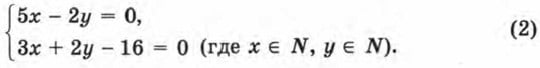§ 11. Основные понятия (продолжение) Алгебра 7 класс Мордкович
Основные понятия. Глава 3. Системы двух линейных уравнений с двумя переменными. Алгебра 7 класс. Мордкович. Учебник
Глава 3. Системы двух линейных уравнений с двумя переменными
Пару значений (х; у), которая одновременно является решением и первого, и второго уравнений системы, называют решением системы.
Решить систему — это значит найти все её решения или установить, что их нет.
Теперь мы можем сказать, что встречались с системой линейных уравнений — математическая модель уже упомянутой задачи про садоводов из § 7 выглядела так:
Её решением была пара (2; 5), т. е. х = 2, у = 5.
Рассмотрим новые примеры.
Пример 1. Решить систему уравнений
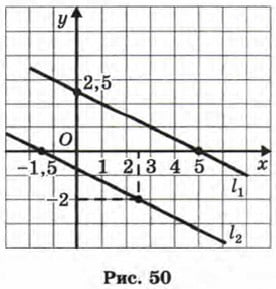
Р е ш е н и е. Графиком уравнения х + 2у – 5 = 0 является прямая. Найдём две пары значений переменных х, у, удовлетворяющих этому уравнению. Если у = 0, то из уравнения х + 2у – 5 = 0 находим х = 5. Если х = 0, то из уравнения х + 2у – 5 = 0 находим у = 2,5. Итак, нашли две точки: (5; 0) и (0; 2,5). Построим на координатной плоскости хОу прямую, проходящую через эти две точки, — прямая l1 на рисунке 50.
Графиком уравнения 2х + 4у + 3 = 0 также является прямая. Найдём две пары значений переменных х, у, удовлетворяющих этому уравнению. Если у = 0, то из уравнения 2х + 4у + 3 = 0 находим х = -1,5. Если х = 2,5, то из уравнения 2х + 4у + 3 = 0 находим 5 + 4у + 3 = 0, и, следовательно, у = -2. Итак, нашли две точки: (-1,5; 0) и (2,5; -2). Построим на координатной плоскости хОу прямую, проходящую через эти две точки, — прямая l2 на рисунке 50.
Прямые l1 и l2 параллельны. Что означает этот геометрический факт для данной системы уравнений? То, что она не имеет решений (поскольку нет точек, удовлетворяющих одновременно и тому и другому уравнению, т. е. принадлежащих одновременно и той и другой из построенных прямых l1 и l2).
О т в е т: система не имеет решений.
Замечание. Если бы мы с самого начала догадались переписать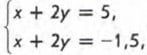 
то сразу было бы очевидно, что решений нет (и соответствующие прямые на самом деле параллельны).
Пример 2. Найти два числа, если известно, что их сумма равна 39, а разность равна 11.
Р е ш е н и е. Если х, у — искомые числа, то х+у = 39 и х - у = 11, причём эти равенства должны выполняться одновременно:
Получили систему двух линейных уравнений с двумя переменными. Можно угадать, чему равны х и у: х = 25, у = 14. Но, во-первых, «метод угадывания» далеко не всегда применим на практике. А во-вторых, где гарантия, что иного решения нет, может быть, мы просто до него не додумались?
Можно построить графики уравнений х + у = 39 и х - у = 11, это прямые, причём непараллельные (в отличие от тех, что в примере 1), они пересекаются в одной точке. Эту точку мы уже знаем: (25; 14); значит, это единственная пара чисел, которая нас устраивает, единственное решение системы.
О т в е т: 25 и 14.