§ 10. Взаимное расположение графиков линейных функций
§ 10. Взаимное расположение графиков линейных функций. Глава 2. Линейная функция. Алгебра 7 класс. Мордкович. Онлайн учебник
Глава 2. Линейная функция
§ 10. Взаимное расположение графиков линейных функций
Вернёмся ещё раз к графикам линейных функций у = 2х – 4 и у = 2х + 6, представленным на рисунке 48. Мы уже отмечали (в § 9), что эти две прямые параллельны прямой у = 2х, а значит, параллельны друг другу. Признаком параллельности служит равенство угловых коэффициентов (k = 2 для всех трёх прямых: и для у = 2х, и для у = 2х – 4, и для у = 2х + 6). Если же угловые коэффициенты различны, как, например, у линейных функций у – 2х и у = 3х + 1, то прямые, служащие их графиками, не параллельны, и тем более не совпадают. Следовательно, указанные прямые пересекаются. Вообще справедлива следующая теорема.
Теорема 5.
|
Пусть даны две линейные функции у = k1x + m1 и у = k2x + m2. Прямые, служащие графиками заданных линейных функций:
|
Пример 1. Найти точку пересечения прямых:
-
а) у = 2х – 3 и
 ;
;б) у = -3х + 1 и у = -3х + 5.
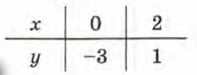
Р е ш е н и е. а) Для линейной функции у = 2х – 3 имеем
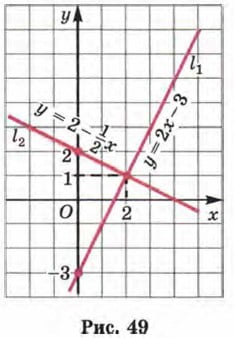
Прямая l1, служащая графиком линейной функции у = 2х – 3, проведена на рисунке 49 через точки (0; -3) и (2; 1).
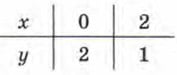
Для линейной функции  имеем
имеем
Прямая l2 служащая графиком линейной функции  проведена на рисунке 49 через точки (0; 2) и (2; 1).
проведена на рисунке 49 через точки (0; 2) и (2; 1).
Прямые l1 и l2 пересекаются в точке (2; 1).
б) Линейные функции у = -3х + 1 и у = -3х + 5 имеют один и тот же угловой коэффициент (k = -3), значит, прямые у = -3х + 1 и у = -3х + 5 параллельны, т. е. точки пересечения у них нет. 
Пример 2. Найти точку пересечения прямых у = 4х + 7 и у = -2х + 7.
Р е ш е н и е. Здесь можно обойтись без чертежа. Будем рассуждать так. Во-первых, угловые коэффициенты прямых различны (k1 = 4, k2 = -2), значит, прямые пересекаются в одной точке.
Во-вторых, как одна, так и другая прямая проходят через точку (0; 7) (вы обратили внимание, что m1 = m2 = 7?).
Следовательно, (0; 7) и есть искомая точка пересечения. 
Вообще прямые у = kx1 + m и у = k2x + m, где k1 ≠ k2, пересекаются в точке (0; m).
Завершая главу 2, обратим внимание на характерную особенность математического языка: во многих фразах, как вы, наверное, заметили, одновременно встречаются элементы алгебраического и геометрического языков — составных частей единого математического языка. Так, мы говорим: точка 3, прямая х = 2, прямая у = -5, прямая у = 2х + 3, отрезок [3; 7], луч [-2; +∞) и т. п. А в § 10 мы получили, пожалуй, наиболее яркие образцы свободного оперирования алгебраическим и геометрическим языками в одном суждении — они представлены в приведённой таблице.

-
Вопросы для самопроверки
1. Приведите пример линейных функций, графики которых параллельны.
2. Приведите пример линейных функций, графики которых совпадают.
3. Приведите пример линейных функций, графики которых пересекаются.
4. Что вы можете сказать о взаимном расположении на координатной плоскости хОу графиков линейных функций:
а) y = 2х + 3 и y = 3х – 2; б) y = 2x + 3 и y = 2x?
5. Как будет расположен график функции у = 4х + а относительно графика функции у = 4x, если а > 0? если а < 0?
6. Сформулируйте теорему о взаимном расположении графиков линейных функций.