§ 1. Числовые и алгебраические выражения (продолжение) Алгебра 7 класс Мордкович

Числовые и алгебраические выражения. Глава 1. Математический язык. Математическая модель. Алгебра 7 класс. Мордкович. Учебник

Глава 1. Математический язык. Математическая модель

3) Разделим с на 4:

Итак, а = -15.

4) В = 25 • 37 • 0,4. Опять-таки можно проводить вычисления «в лоб», т. е. вычислить 25*37, затем то, что получится, умножить на 0,4. Но думающий человек (а таким всегда является культурный человек) воспользуется переместительным и сочетательным законами умножения и будет вычислять так:

• 25 • 37 0,4 = (25 • 0,4) • 37 = 10 • 37 = 370.

Итак, b = 370.

5) Осталось разделить числитель а на знаменатель b. Получим (разделили числитель и знаменатель дроби на 5, т. е. сократили дробь).

О т в е т:

А теперь вместе проанализируем, какие сведения из математики нам пришлось вспомнить в процессе решения примера (причём не просто вспомнить, но и использовать).

1. Порядок арифметических действий.

2. Переместительный закон сложения: а + b = b + а.

3. Переместительный закон умножения: аb = bа.

4. Сочетательный закон сложения:

• а + b + с = (а + b) + с = а + (b + с).

5. Сочетательный закон умножения: аbс = (ab)c = а(bс).

6. Понятия обыкновенной дроби, десятичной дроби, отрицательного числа.

7. Арифметические операции с десятичными дробями.

8. Арифметические операции с обыкновенными дробями.

9. Основное свойство обыкновенной дроби: 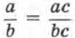(значение дроби не изменится, если её числитель и знаменатель одновременно умножить на одно и то же число или разделить на одно и то же число, отличное от нуля). Это свойство позволило нам преобразовать дробь к виду 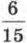(числитель и знаменатель дроби одновременно умножили на одно и то же число 3). Оно же позволило нам сократить дробь (числитель и знаменатель дроби одновременно разделили на одно и то же число 5).

10. Правила действий с положительными и отрицательными числами.

Всё это вы знаете, но ведь всё это — алгебраические факты. Таким образом, некоторое знакомство с алгеброй у вас уже состоялось в младших классах. Основная трудность, как видно уже из примера 1, заключается в том, что таких фактов довольно много, причём их надо не только знать, но и уметь использовать, как говорят, «в нужное время и в нужном месте». Вот этому и будем учиться.

И последнее, чтобы закончить обсуждение примера 1. То число, которое получается в результате упрощений числового выражения (в данном примере это было число называют значением числового выражения.

Если дано алгебраическое выражение, то можно говорить о значении алгебраического выражения, но только при конкретных значениях входящих в него букв. Например, алгебраическое выражение а + b при а = 5, b = 7 имеет значение 12 (поскольку а + b = 5 + 7 = 12); при а = -16, b = -14 оно имеет значение -30 (так как а + b = -16 + (-14) = -16 – 14 = -30). Алгебраическое выражение а² – 3b (что такое а², помните? — это а • а) при а = -2, b = 0,4 принимает вид числового выражения (-2)² – 3 • 0,4; упрощая, получаем 4 – 1,2 = 2,8 — это и есть значение алгебраического выражения а² – 3b при а = -2, b = 0,4.

Поскольку буквам, входящим в состав алгебраического выражения, можно придавать различные числовые значения (т.е. можно менять значения букв), эти буквы называют переменными.