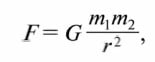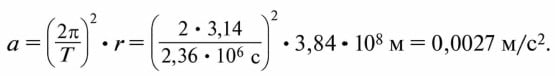Закон всемирного тяготения
Закон всемирного тяготения. § 14. Движение небесных тел под действием сил тяготения. Астрономия 11 класс. Воронцов-Вельяминов. Онлайн учебник
§ 14. Движение небесных тел под действием сил тяготения
Закон всемирного тяготения
Согласно закону всемирного тяготения, изученному в курсе физики,
-
все тела во Вселенной притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними:
где m1 и m2 — массы тел; r — расстояние между ними; G — гравитационная постоянная.
Открытию закона всемирного тяготения во многом способствовали законы движения планет, сформулированные Кеплером, и другие достижения астрономии XVII в. Так, знание расстояния до Луны позволило Исааку Ньютону (1643—1727) доказать тождественность силы, удерживающей Луну при ее движении вокруг Земли, и силы, вызывающей падение тел на Землю.
Ведь если сила тяжести меняется обратно пропорционально квадрату расстояния, как это следует из закона всемирного тяготения, то Луна, находящаяся от Земли на расстоянии примерно 60 её радиусов, должна испытывать ускорение в 3600 раз меньшее, чем ускорение силы тяжести на поверхности Земли, равное 9,8 м/с2. Следовательно, ускорение Луны должно составлять 0,0027 м/с2.
В то же время Луна, как любое тело, равномерно движущееся по окружности, имеет ускорение
-
а = ω2r,
где ω — угловая скорость Луны; r — радиус её орбиты. Если считать, что радиус Земли равен 6400 км, то радиус лунной орбиты будет составлять r = 60 • 6 400 000 м = 3,84 • 108 м. Звёздный период обращения Луны Т = 27,32 суток, в секундах составляет 2,36 • 106 с. Тогда ускорение орбитального движения Луны
Равенство этих двух величин ускорения доказывает, что сила, удерживающая Луну на орбите, есть сила земного притяжения, ослабленная в 3600 раз по сравнению с действующей на поверхности Земли.
Можно убедиться и в том, что при движении планет, в соответствии с третьим законом Кеплера, их ускорение и действующая на них сила притяжения Солнца обратно пропорциональны квадрату расстояния, как это следует из закона всемирного тяготения. Действительно, согласно третьему закону Кеплера отношение кубов больших полуосей орбит d и квадратов периодов обращения Т есть величина постоянная:
Ускорение планеты равно
Из третьего закона Кеплера следует
поэтому ускорение планеты равно
Итак, сила взаимодействия планет и Солнца удовлетворяет закону всемирного тяготения.