Функция у = √x и её график (продолжение)

Функция у = √x и её график. § 5. Арифметический квадратный корень. Алгебра 8 класс. Макарычев. Онлайн учебник

§ 5. Арифметический квадратный корень

Функция у = √x и её график (продолжение)

График функции у = √х, как и график функции у = х², где х ≥ 0, представляет собой ветвь параболы. Эти графики симметричны относительно прямой у = х (рис. 18). Доказательство симметрии графиков основано на том, что точки с координатами (а; b) и (b; а) симметричны относительно прямой у = х.

Пусть точка М(а; b) принадлежит графику функции у = х², где х ≥ 0. Тогда верно равенство b = а². По условию а — неотрицательное число, поэтому а = √b. Значит, при подстановке координат точки N (b; а) в формулу у = √х получается верное равенство, т. е. точка N (b; а) принадлежит графику функции у = √x. Верно и обратное: если некоторая точка принадлежит второму графику, то точка, у которой координатами являются те же числа, но взятые в другом порядке, принадлежит первому графику.

Таким образом, каждой точке М(а; b) графика функции у = х², где х ≥ 0, соответствует точка N (b; а) графика функции у = √x и наоборот. Так как точки М (а; b) и N (b; а) симметричны относительно прямой у = х, то и сами графики симметричны относительно этой прямой.

Упражнения

352. Площадь круга может быть вычислена по формуле S = πr², где r — радиус круга, или по формуле 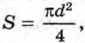где d — диаметр круга. Задайте формулой зависимость:

• а) r от S; б) d от S.

353. Задайте формулой зависимость:

• а) площади поверхности куба S от длины его ребра а;
  
  б) длины ребра куба а от площади его поверхности S.

354. Площадь поверхности шара радиуса R вычисляется по формуле S = 4πR². Задайте формулой зависимость R от S.

355. Пользуясь графиком функции у = √x, найдите:

• а) значение √x при х = 2,5; 5,5; 8,4;
  
  б) значение х, которому соответствует √х = 1,2; 1,7; 2,5.

356. С помощью графика функции у = √x найдите:

• а) значение функции при х = 0,5; 1,5; 6,5; 7,2;
  
  б) значение аргумента, которому соответствует значение y = 0,5; 1,5; 1,8; 2,3.

357. Принадлежит ли графику функции у = √x точка А (64; 8)? точка В(10 000; 100)? точка С(-81; 9)? точка D(25; -5)?

358. Пересекает ли график функции у = √x прямая:

• а) у = 1; б) у = 10;

  в) у = 100; г) у = -100?

Если пересекает, то в какой точке?

359. Докажите, что графики функций у = √x и у = х + 0,5 не имеют общих точек.

360. (Для работы в парах.) Имеют ли общие точки графики функций:

• а) у = √x и у = х; б) у = √x и у = 1000;

  в) у = √x и у = х + 10; г) у = √x и у = -х + 1,5?

При положительном ответе укажите координаты этих точек.

• 1) Распределите, кто выполняет задания а) и в), а кто — задания б) и г), и выполните их.
  
  2) Проверьте друг у друга, верно ли выполнены задания. Исправьте замеченные ошибки.
  
  3) Приведите примеры линейных функций, графики которых: не пересекают график функции у = √x; пересекают его в одной точке; пересекают его в двух точках. Обсудите правильность этих примеров.

<<< К началу          Окончание >>>