Решение неравенств методом интервалов

Решение неравенств методом интервалов. § 6. Неравенства с одной переменной. Алгебра 9 класс. Макарычев

§ 6. Неравенства с одной переменной

Решение неравенств методом интервалов

Рассмотрим функцию

• ƒ(x) = (х + 2)(х – 3)(x – 5).

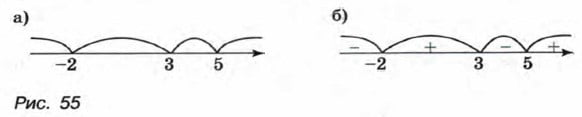
Областью определения этой функции является множество всех чисел. Нулями функции служат числа -2, 3, 5. Они разбивают область определения функции на промежутки (-∞; -2), (-2; 3), (3; 5) и (5; +∞) (рис. 55, а).

Выясним, каковы знаки этой функции в каждом из указанных промежутков.

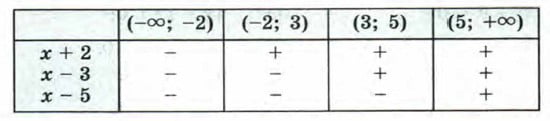
Выражение (х + 2) (х – 3) (х – 5) представляет собой произведение трех множителей. Знак каждого из этих множителей в рассматриваемых промежутках указан в таблице:

Отсюда ясно, что:

• если х ∈ (-∞; -2), то ƒ(x) < 0;
  если х ∈ (-2; 3), то ƒ(x) > 0;
  
  если х ∈ (3; 5), то ƒ(x) < 0;
  если х ∈ (5; +∞), то ƒ(x) > 0.

Мы видим, что в каждом из промежутков (-∞; -2), (-2; 3), (3; 5), (5; +∞) функция сохраняет знак, а при переходе через точки -2, 3 и 5 ее знак изменяется (рис. 55, б).

Вообще пусть функция задана формулой

• ƒ(x) = (х – х₁)(х – х₂) … (х – х_n),

где х— переменная, а х₁, х₂, …, х_n — не равные друг другу числа. Числа х₁, х₂, …, х_n являются нулями функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль ее знак изменяется.

Это свойство используется для решения неравенств вида

где x₁, х₂, …, х_n — не равные друг другу числа.

Пример 1. Решим неравенство (х + 6)(х + 1)(х – 4) < 0.

Это неравенство является неравенством вида (1), так как в левой части записано произведение (х – х₁)(х – х₂)(х – х₃), где х₁ = -6, х₂ = -1 и х₃ = 4. Для его решения удобно воспользоваться рассмотренным выше свойством чередования знаков функции. Отметим на координатной прямой нули функции

• ƒ(х) = (х + 6)(х + 1)(х – 4)

(рис. 56, а). Найдем знаки этой функции в каждом из промежутков (-∞; -6), (-6; -1), (-1; 4) и (4; +∞). Для этого достаточно знать, какой знак имеет функция в одном из этих промежутков, и, пользуясь свойством чередования знаков, определить знаки во всех остальных промежутках. При этом удобно начинать с крайнего справа промежутка (4; +∞), так как в нем значения функции ƒ(х) = (х + 6) (х + 1) (х – 4) заведомо положительны. Это объясняется тем, что при значениях х, расположенных правее всех нулей функции, каждый из множителей х + 6, х + 1 и х-4 положителен. Используя свойство чередования знаков, определим, двигаясь по координатной прямой справа налево, знаки данной функции в каждом из остальных промежутков (рис. 56, б).

Из рисунка видно, что множеством решений неравенства является объединение промежутков (-∞; — 6) и (-1; 4).

Ответ: (-∞; -6) ∪ (-1; 4).

Рассмотренный способ решения неравенств называют методом интервалов.

Приведем примеры решения неравенств методом интервалов.

Продолжение >>>