§ 31. Вынесение общего множителя за скобки (окончание)
Вынесение общего множителя за скобки. Глава 7. Разложение многочленов на множители. Алгебра 7 класс. Онлайн учебник. Мордкович
Глава 7. Разложение многочленов на множители
§ 31. Вынесение общего множителя за скобки (окончание)
Пример 2. Разложить на множители многочлен
-
-х4у3 – 2х3у2 + 5х2.
Р е ш е н и е.
Воспользуемся сформулированным алгоритмом.

1) Наибольший общий делитель коэффициентов -1, -2 и 5 равен 1.
2) Переменная х входит во все члены многочлена с показателями соответственно 4, 3, 2; следовательно, можно вынести за скобки х2.
Переменная у входит не во все члены многочлена; значит, её нельзя вынести за скобки.
3) В ы в о д: за скобки можно вынести х2. Правда, в данном случае целесообразнее вынести за скобки -х2. Получим
-
-x4y3 – 2х3у2 + 5х2 = -х(х2у3 + 2ху2 – 5).

Пример 3. Можно ли разделить многочлен 5а4 – 10а3 + 15а5 на одночлен: а) 5а3; б) 25а2? Если да, то выполнить деление.
Р е ш е н и е.
а) В примере 1д) мы получили, что
-
5а4 – 10а3 + 15а5 = 5а3(а -2 + 3а2).
Значит, заданный многочлен можно разделить на 5а3, при этом в частном получится а – 2 + 3а2.
Значит, заданный многочлен можно разделить на 25а2, при этом в частном получится 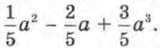


Подобные примеры мы рассматривали в § 29; просмотрите их, пожалуйста, ещё раз, но уже с точки зрения вынесения общего множителя за скобки.
Разложение многочлена на множители с помощью вынесения общего множителя за скобки тесно связано с двумя операциями, которые мы изучали в § 26 и 29, — с умножением многочлена на одночлен и с делением многочлена на одночлен.
А теперь несколько расширим наши представления о вынесении общего множителя за скобки. Дело в том, что иногда алгебраическое выражение задаётся в таком виде, что в качестве общего множителя может выступать не одночлен, а сумма нескольких одночленов.
Пример 4. Разложить на множители
-
2х(х – 2) + 5(х – 2)2.
Р е ш е н и е.
Введём новую переменную у = х – 2. Тогда получим
-
2х(х – 2) + 5(х – 2)2 = 2xy + 5у2.
Замечаем, что переменную у можно вынести за скобки: 2ху + 5у2 = у(2х + 5у). А теперь вернёмся к старым обозначениям:
-
у(2х + by) = (х – 2)(2х + 5(х – 2)) = (х – 2)(2х + bх – 10) = (х – 2)(7х – 10).
В подобных случаях после приобретения некоторого опыта можно не вводить новую переменную, а использовать следующую запись:
-
2х(х – 2) + 5(х – 2)2 = (х – 2)(2х + 5(х – 2)) = (х – 2) (2х + 5х – 10) = (х – 2)(7х – 10).

-
Вопросы для самопроверки
1. Как вы понимаете, что означает процесс вынесения множителя за скобки?
2. Сформулируйте алгоритм отыскания общего множителя нескольких одночленов.
3. Приведите пример трёхчлена, у которого можно вынести за скобки общий множитель 3х2.
<<< К началу
