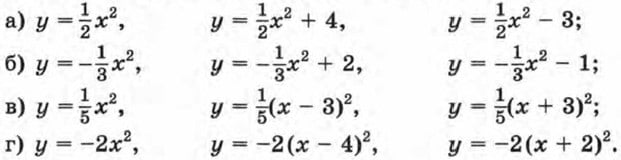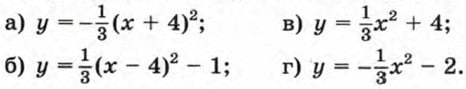Графики функций у = ах2 + n и у= а(х – m)2 (окончание)
Графики функций у = ах2 + n и у= а(х – m)2 (окончание). § 3. Квадратичная функция и ее график. Алгебра 9 класс. Макарычев. Ответы
2 + n и у= а(х – m)2 (окончание). § 3. Квадратичная функция и ее график. Алгебра 9 класс. Макарычев”>
§ 3. Квадратичная функция и ее график
Графики функций у = ах2 + n и у= а(х – m)2 (окончание)
Упражнения
106. Изобразите схематически график каждой функции (отметьте вершину параболы и направление ее ветвей):
107. С помощью шаблона параболы у = х2 постройте график функции:
-
а) у = х2 – 4;
б) у = -х2 + 3;в) у = (х – 5)2;
г) у = (х + З)2.
108. Используя шаблон параболы у = х2, постройте график функции:
-
а) у = х2 + 2;
б) у = -x2 – 1;в) у = (х + 4)2;
г) у = -(х – 3)2.
109. В каких координатных четвертях расположен график функции:
-
а) у = 10х2 + 5;
б) у = -7х2 – 3;
в) у = -6х2 + 8;г) у = (х – 4)2;
д) у = -(х – 8)2;
е) у = -3(х + 5)2?
110. Изобразите схематически график функции:
111. Изобразите схематически график функции:
112. Используя шаблон параболы у = х2, постройте график функции:
-
а) у = (х – 2)2 + 3; б) у = -(х – 3)2 + 5.
113. С помощью шаблона параболы у = х2 постройте график функции:
-
а) у = (х + З)2 – 4; б) у = -(х + 4)2 – 2.
114. Найдите нули функции (если они существуют):
-
а) у = 12х2 – 3; б) у = 6х2 + 4; в) у = -х2 – 4.
115. При каких значениях а функция у = ах2 + 5 имеет нули?
116. На рисунке 30 изображены графики функций:
Для каждого графика укажите соответствующую формулу.
Повторение
117. Решите уравнение:
-
а) 0,6а – (а + 0,3)2 = 0,27;
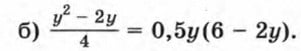
118. Решите неравенство:
-
а) 5х – 0,7 < 3х + 5,1;
б) 0,8д: + 4,5 ≥ 5 – 1,2х;в) 2х + 4,2 ≤ 4х + 7,8;
г) Зх – 2,6 > 5,5х – 3,1.
119. Найдите приращение функции у = х2 при изменении х от 2 до 5 и от 5 до 8. Сравните полученные результаты.
Ответы
-
114.
б) нулей нет; в) нулей нет.115. При а < 0.
117. а) Корней нет; б) 0; 2,8.
118. а) (-∞; 2,9); б) [0,25; +∞); в) [-1,8; +∞); г) (-∞; 0,2).
2 + n и у= а(х – m)2“> <<< К началу