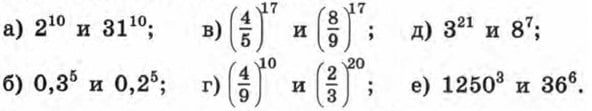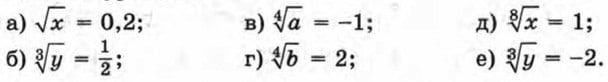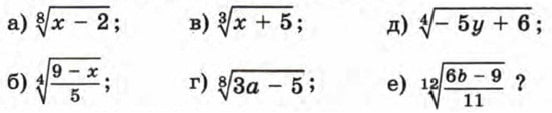К параграфу 4

К параграфу 4. Дополнительные упражнения к главе I. Алгебра 9 класс. Макарычев. Ответы

Дополнительные упражнения к главе I

К параграфу 4

249. Объясните, почему верно неравенство:

250. Сравните значения степеней:

251. Даны функции ƒ(x) = х⁷ и g(x) = x¹⁰. Сравните с нулем:

• а) ƒ(25) – ƒ(12); б) ƒ(-30) – ƒ(-20); в) ƒ(0) • ƒ(60);

  г) g(17) – g(5); д) g(-9) • g(-17); е) g(38) – g(0).

252. Докажите, что при натуральном n:

• а) если х∈ [0; 1], то хⁿ + 1 ≤ хⁿ;
  
  б) если х∈ (1; +∞), то хⁿ + 1 > хⁿ.

253. Найдите n, если известно, что график функции у = хⁿ проходит через точку:

• а) А(2; 8); б) В(3,5; 12,25); в) С(-3; 81); г) D(-2; -32).

254. Существует ли такое натуральное значение п, при котором график функции у = хⁿ проходит через точку:

• а) А(2; 5); б) B(√3; 81); в) С(-5; 415); г) D(-7; -343)?

255. Постройте график функции:

• а) у = -x3; б) у = х3 – 1; в) у = (х – 2)3; г) у = (х – 2)3 +1;

  д) у = -х4; е) у = х4 – 1; ж) у = (х – 3)4; з) у = (х – 3)4 + 2.

256. Сколько корней имеет уравнение:

• а) х10 = 2; б) х10 = 0; в) х10 = -3;

  г) х7 = 5; д) x7 = 0; е) х7 = -1?

257. Найдите значение выражения:

258. Решите уравнение:

259. При каких значениях переменной имеет смысл выражение:

260. Сравните значения корней:

261. Определите знак разности:

262. Найдите область определения функции:

263. Пользуясь графиками функций у = х, у = √x, решите уравнение и неравенства:

264. Постройте график функции:

Чем отличаются друг от друга графики функций у = – √x и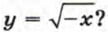

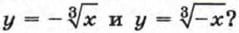
Ответы

• 257. в) 3; г) 3,5; д) -0,5; е)

  259. г) При 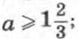е) при b ≥ 1,5.